Overview
The main concepts of information theory can be grasped by considering the most widespread means of human communication: language. Two important aspects of a concise language are as follows: First, the most common words (e.g., "a", "the", "I") should be shorter than less common words (e.g., "benefit", "generation", "mediocre"), so that sentences will not be too long. Such a tradeoff in word length is analogous to data compression and is the essential aspect of source coding. Second, if part of a sentence is unheard or misheard due to noise — e.g., a passing car — the listener should still be able to glean the meaning of the underlying message. Such robustness is as essential for an electronic communication system as it is for a language; properly building such robustness into communications is done by channel coding. Source coding and channel coding are the fundamental concerns of information theory.
Note that these concerns have nothing to do with the importance of messages. For example, a platitude such as "Thank you; come again" takes about as long to say or write as the urgent plea, "Call an ambulance!" while the latter may be more important and more meaningful in many contexts. Information theory, however, does not consider message importance or meaning, as these are matters of the quality of data rather than the quantity and readability of data, the latter of which is determined solely by probabilities.
Information theory is generally considered to have been founded in 1948 by Claude Shannon in his seminal work, "A Mathematical Theory of Communication". The central paradigm of classical information theory is the engineering problem of the transmission of information over a noisy channel. The most fundamental results of this theory are Shannon's source coding theorem, which establishes that, on average, the number of bits needed to represent the result of an uncertain event is given by its entropy; and Shannon's noisy-channel coding theorem, which states that reliablecommunication is possible over noisy channels provided that the rate of communication is below a certain threshold called the channel capacity. The channel capacity can be approached in practice by using appropriate encoding and decoding systems.
Information theory is closely associated with a collection of pure and applied disciplines that have been investigated and reduced to engineering practice under a variety of rubrics throughout the world over the past half century or more: adaptive systems, anticipatory systems, artificial intelligence, complex systems, complexity science, cybernetics, informatics, machine learning, along with systems sciences of many descriptions. Information theory is a broad and deep mathematical theory, with equally broad and deep applications, amongst which is the vital field of coding theory.
Coding theory is concerned with finding explicit methods, called codes, of increasing the efficiency and reducing the net error rate of data communication over a noisy channel to near the limit that Shannon proved is the maximum possible for that channel. These codes can be roughly subdivided into data compression (source coding) and error-correction (channel coding) techniques. In the latter case, it took many years to find the methods Shannon's work proved were possible. A third class of information theory codes are cryptographic algorithms (both codes and ciphers). Concepts, methods and results from coding theory and information theory are widely used in cryptography and cryptanalysis. See the article ban (information) for a historical application.
Information theory is also used in information retrieval, intelligence gathering, gambling, statistics, and even in musical composition.





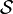 = (S,P) with
= (S,P) with 


 or
or  , is defined as the
, is defined as the 
 the binary entropy function attains its maximum value. This is the case of the unbiased
the binary entropy function attains its maximum value. This is the case of the unbiased