Neelesh

Thursday, July 29, 2010

A common way to define entropy for text is based on the Markov model of text. For an order-0 source (each character is selected independent of the last characters), the binary entropy is:

$H(\mathcal{S}) = - \sum p_i \log_2 p_i, \,\!$

where p_i is the probability of i. For a first-order Markov source (one in which the probability of selecting a character is dependent only on the immediately preceding character), the entropy rate is:

$H(\mathcal{S}) = - \sum_i p_i \sum_j \ p_i (j) \log_2 p_i (j), \,\!$

where i is a state (certain preceding characters) and

p i (j)

is the probability of

j

given

i

as the previous character.

For a second order Markov source, the entropy rate is

$H(\mathcal{S}) = -\sum_i p_i \sum_j p_i(j) \sum_k p_{i,j}(k)\ \log_2 \ p_{i,j}(k). \,\!$

[edit]b-ary entropy

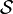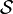In general the b-ary entropy of a source $\mathcal{S}$ = (S,P) with source alphabet S = {a₁, ..., a_n} and discrete probability distribution P = {p₁, ..., p_n} where p_i is the probability of a_i (say p_i = p(a_i)) is defined by:

$H_b(\mathcal{S}) = - \sum_{i=1}^n p_i \log_b p_i, \,\!$

Note: the b in "b-ary entropy" is the number of different symbols of the "ideal alphabet" which is being used as the standard yardstick to measure source alphabets. In information theory, two symbols are necessary and sufficient for an alphabet to be able to encode information, therefore the default is to let b = 2 ("binary entropy"). Thus, the entropy of the source alphabet, with its given empiric probability distribution, is a number equal to the number (possibly fractional) of symbols of the "ideal alphabet", with an optimal probability distribution, necessary to encode for each symbol of the source alphabet. Also note that "optimal probability distribution" here means a uniform distribution: a source alphabet with n symbols has the highest possible entropy (for an alphabet with n symbols) when the probability distribution of the alphabet is uniform. This optimal entropy turns out to be $\log_b \, n$